Optimizing Structures and Materials

Narrow-Band Topology Optimization on a Sparsely Populated Grid

Abstract: A variety of structures in nature exhibit sparse, thin, and intricate features. It is challenging to investigate these structural characteristics using conventional numerical approaches since such features require highly refined spatial resolution to capture and therefore they incur a prohibitively high computational cost. We present a novel computational framework for high-resolution topology optimization that delivers leaps in simulation capabilities, by two orders of magnitude, from the state-of-the-art approaches. Our technique accommodates computational domains with over one billion grid voxels on a single shared-memory multiprocessor platform, allowing automated emergence of structures with both rich geometric features and exceptional mechanical performance. To achieve this, we track the evolution of thin structures and simulate its elastic deformation in a dynamic narrow-band region around high-density sites to avoid wasted computational effort on large void regions. We have also designed a mixed-precision multigrid-preconditioned iterative solver that keeps the memory footprint of the simulation to a compact size while maintaining double-precision accuracy. We have demonstrated the efficacy of the algorithm through optimizing a variety of complex structures from both natural and engineering systems.

Authors/Presenter(s): Haixiang Liu, University of Wisconsin–Madison, United States of America
Yuanming Hu, MIT CSAIL, United States of America
Bo Zhu, MIT CSAIL, Dartmouth College, United States of America
Wojciech Matusik, MIT CSAIL, United States of America
Eftychios Sifakis, University of Wisconsin–Madison, United States of America

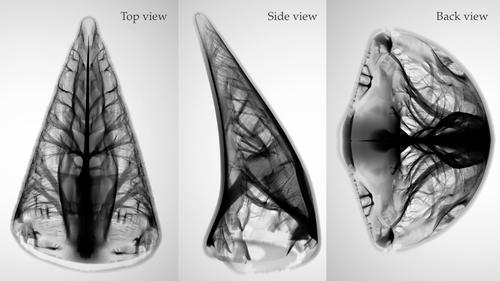
Set-In-Stone: Worst-Case Optimization of Structures Weak in Tension

Abstract: Large-scale binder jetting provides a promising alternative to manual sculpting of sandstone. The weak build material, however, severely limits its use in architectural ornamentation. We propose a structural optimization that jointly optimizes an ornament's strength-to-weight ratio and balance under self-weight, thermal, wind, and live loads. To account for the difference in the tensile and compressive strength of the build material, we turn the Bresler-Pister criterion into a failure potential, measuring the distance to failure. Integrated into an XFEM-based level set formulation, we minimize this potential by changing the topology and shape of the internal structure. To deal with uncertainties in the location of live loads, and the direction of wind loads, we first estimate loads that lead to the weakest structure, then minimize the potential of failure under identified worst-case loads. With the help of first-order optimality constraints, we unify our worst-case load estimation and structural optimization into a continuous optimization. We demonstrate applications in art, furniture design, and architectural ornamentation with three large-scale 3D printed examples.

Authors/Presenter(s): Christian Schumacher, Disney Research, Switzerland
Jonas Zehnder, Disney Research, Université de Montréal, Canada
Moritz Bächer, Disney Research, Switzerland

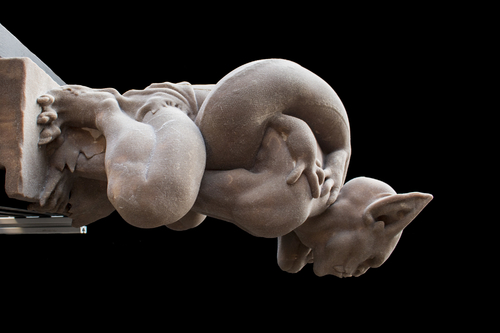
Inexact Descent Methods for Elastic Parameter Optimization

Abstract: Elastic parameter optimization has revealed its importance in 3D modeling, virtual reality, and additive manufacturing applications in recent years. Unfortunately, it is known to be computationally expensive, especially if there are many parameters and data samples. To address this challenge, we propose to introduce the inexactness into descent methods, by iteratively solving a forward simulation step and a parameter update step in an inexact manner. The development of such inexact descent methods is centered at two questions: 1) how accurate/inaccurate can the two steps be; and 2) what is the optimal way to implement an inexact descent method. The answers to these questions are in our convergence analysis, which proves the existence of relative error thresholds for the two inexact steps to ensure the convergence. This means we can simply solve each step by a fixed number of iterations, if the iterative solver is at least linearly convergent. While the use of the inexact idea speeds up many descent methods, we specifically favor a GPU-based one powered by state-of-the-art simulation techniques. Based on this method, we study a variety of implementation issues, including backtracking line search, initialization, regularization, and multiple data samples. We demonstrate the use of our inexact method in elasticity design and measurement applications. The experiment shows the method is fast, reliable, memory-efficient, GPU-friendly, flexible with different elastic models, scalable to a large parameter space, and parallelizable for multiple data samples.

Authors/Presenter(s): Guowei Yan, The Ohio State University, United States of America
Wei Li, University of Kentucky, United States of America
Ruigang Yang, University of Kentucky, United States of America
Huamin Wang, The Ohio State University, United States of America

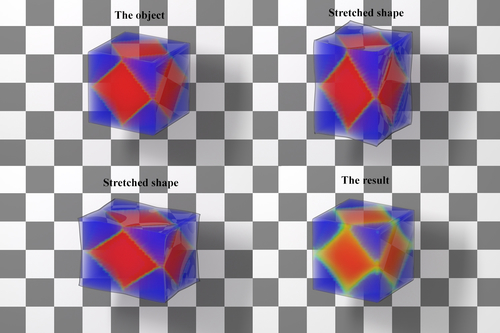
GPU Optimization of Material Point Methods

Abstract: The Material Point Method (MPM) has been shown to facilitate effective simulations of physically complex and topologically challenging materials, with a wealth of emerging applications in computational engineering and visual computing. Borne out of the extreme importance of regularity, MPM is given attractive parallelization opportunities on high-performance modern multiprocessors. Unlike the conceptually simple CPU parallelization, a GPU optimization of MPM that fully leverages computing resources presents challenges that require exploring an extensive design-space for favorable data structures and algorithms. In this paper, we introduce methods for addressing the computational challenges of MPM and extending the capabilities of general simulation systems based on MPM, particularly concentrating on GPU optimization. In addition to our open-source high-performance framework, we also perform performance analyses and benchmark experiments to compare against alternative design choices which may superficially appear to be reasonable, but can suffer from suboptimal performance in practice. Our explicit and fully implicit GPU MPM solvers are further equipped with a Moving Least Squares MPM heat solver and a novel sand constitutive model to enable fast simulations of a wide range of materials. We demonstrate that more than an order of magnitude performance improvement can be achieved with our GPU solvers. Practical high-resolution examples with up to ten million particles run in less than one minute per frame.

Authors/Presenter(s): Ming Gao, University of Wisconsin, Madison, United States of America
Xinlei Wang, Zhejiang University, China
Kui Wu, The University of Utah, United States of America
Andre Pradhana, University of Pennsylvania, United States of America
Eftychios Sifakis, University of Wisconsin, Madison, United States of America
Cem Yuksel, The University of Utah, United States of America
Chenfanfu Jiang, University of Pennsylvania, United States of America