Nets, Cages and Meshes

Approximate Convex Decomposition and Transfer for Animated Meshes

Abstract: Many geometric quantities can be computed efficiently for convex meshes. For general meshes, methods for approximate convex decomposition have been developed that decompose a static, non-convex object into a small set of approximately convex parts. The convex hulls of those parts can then be used as a piecewise convex approximation to the original mesh. While previous work was only concerned with static meshes, we present a method for decomposing animated 3D meshes into temporally coherent approximately convex parts. Given a mesh and several training frames---that is, different spatial configurations of its vertices---we precompute an approximate convex decomposition that is independent of any specific frame. Such a decomposition can be transferred in real-time to novel, unseen frames. We apply our method to a variety of pre-animated meshes as well as a 3D character interactively controlled by a user's body pose. We further demonstrate that our method enables real-time physics simulations to interact with animated meshes.

Authors/Presenter(s): Daniel Thul, ETH Zurich, Switzerland
Lubor Ladicky, ETH Zurich, Apagom AG, Switzerland
SoHyeon Jeong, Apagom AG, Switzerland
Marc Pollefeys, ETH Zurich, Microsoft, Switzerland

Canonical Moebius Subdivision

Abstract: We present a novel framework for creating Moebius-invariant subdivision operators with a simple conversion of existing linear subdivision operators. By doing so, we create a wide variety of subdivision surfaces that have properties derived from Moebius geometry; namely, reproducing spheres, circular arcs, and Moebius regularity. Our method is based on establishing a canonical form for each 1-ring in the mesh, representing the class of all 1-rings that are Moebius equivalent to that 1-ring. We perform a chosen linear subdivision operation on these canonical forms, and blend the positions contributed from adjacent 1-rings, using two novel Moebius-invariant operators, into new face and edge points. The generality of the method allows for easy coarse-to-fine mesh editing with diverse polygonal patterns, and with exact reproduction of circular and spherical features. Our operators are in closed-form and their computation is as local as the computation of the linear operators they correspond to, allowing for efficient subdivision mesh editing and optimization.

Authors/Presenter(s): Amir Vaxman, Utrecht University, Netherlands
Christian Mueller, TU Wien, Caltech, Austria
Ofir Weber, Bar-Ilan University, Israel

The Shape Space of Discrete Orthogonal Geodesic Nets

Abstract: Discrete orthogonal geodesic nets (DOGs) are a quad mesh analogue of developable surfaces. In this work we study continuous deformations on these discrete objects. Our main theoretical contribution is the characterization of the shape space of DOGs for a given net connectivity. We show that this space is locally a manifold of a fixed dimension, apart from a sparse set of singularities, implying that DOGs are continuously deformable. Smooth flows can be constructed by a smooth choice of vectors on the manifold’s tangent spaces, selected to minimize a desired objective function under a given metric. We show how to compute such vectors by solving a linear system, and we use our findings to devise a geometrically meaningful way to handle singular points. We base our shape space metric on a novel DOG Laplacian operator, which is proved to converge under sampling of an analytical orthogonal geodesic net. We further show how to extend the shape space of DOGs by supporting creases and curved folds and apply the developed tools in an editing system for developable surfaces that supports arbitrary bending, stretching, cutting, (curved) folds, as well as smoothing and subdivision operations.

Authors/Presenter(s): Michael Rabinovich, ETH Zurich, Switzerland
Tim Hoffmann, TU Munich, Germany
Olga Sorkine-Hornung, ETH Zurich, Switzerland

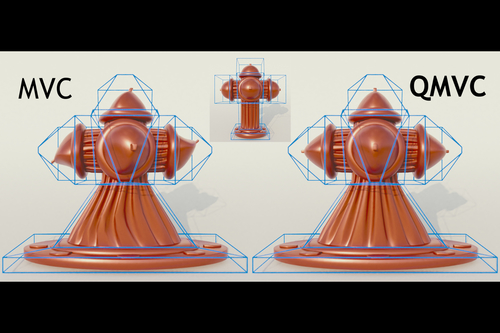
Mean value coordinates for quad cages in 3D

Abstract: Space coordinates offer an elegant, scalable and versatile framework to propagate (multi-)scalar functions from the boundary vertices of a 3-manifold, often called a cage, within its volume. These generalizations of the barycentric coordinate system have progressively expanded the range of eligible cages to triangle surface meshes with arbitrary topology, concave regions and a spatially-varying sampling ratio, while preserving a smooth diffusion of the prescribed on-surface functions. In spite of their potential for major computer graphics applications such as freeform deformation or volume texturing, current space coordinate systems have only found a moderate impact in applications. This follows from the constraint on having only triangles in the cage, while many application scenarios favor quad meshes for their ability to align the surface structure with features and to naturally cope with anisotropic sampling. In order to use space coordinates with quad cages, one must triangulate them, which results in large propagation distorsion. Instead, we propose a generalization of a popular coordinate system – Mean Value Coordinates – to quad and tri-quad cages, bridging the gap between high-quality coarse meshing and volume diffusion through space coordinates. Our method can process non-planar quads, comes with a closed-form solution free from global optimization and reproduces the expected behavior of Mean Value Coordinates, namely smoothness within the cage volume and continuity everywhere. As a result, we show how these coordinates compare favorably to classical space coordinates on triangulated quad cages, in particular for freeform deformation and volumetric texturing.

Authors/Presenter(s): Jean-Marc Thiery, Telecom ParisTech, France
Pooran Memari, Polytechnique, LIX, France
Tamy Boubekeur, Telecom-ParisTech, LTCI, France

Factor once: Reusing Cholesky factorizations on sub-meshes

Abstract: A common operation in geometry processing involves solving symmetric, positive definite systems on a subset of a mesh, with conditions for the vertices on the boundary of the region. This is commonly done by setting up the linear system for the sub-mesh, factorizing the system (potentially applying preordering to improve sparseness of the factors), and then solving by back-substitution. This approach suffers from a comparably high setup cost for each local operation. We propose to reuse factorizations defined on the full mesh to solve linear problems on sub-meshes. We show how this update on sparse matrices can be performed in a particularly efficient way, significantly outperforming general factor updates. We analyze the resulting speed-up for a variety of situations and demonstrate that our method outperforms factorization of a new matrix by a factor of up to 10 while never beeing slower in our experiments.

Authors/Presenter(s): Philipp Herholz, TU Berlin, Germany
Marc Alexa, TU Berlin, Germany